Options Greek Cheat Sheet

This cheat sheet provides an intermediate-level explanation of the five standard options Greeks: Delta, Gamma, Theta, Vega, and Rho. Each section includes definitions, characteristics, practical examples, and visual representations to help you understand how these metrics affect option prices and trading strategies.

Delta (Δ)

>Δ Definition

Delta is often said to be the most important of the Greeks. It measures the change in an option's price from a change in the underlying security.

Characteristics

• For call options, delta ranges from 0 to +1.00
• For put options, delta ranges from 0 to -1.00
• A delta of 0.50 means the option price will move about 50 cents for every $1 change in the stock price

Practical Example

If you own a call option with a delta of 0.40 and the stock price increases by $1, your option should gain about 40 cents in value (provided the other Greeks remain the same).

The opposite happens if the stock falls—you'd lose about 40 cents.

Delta as an Indicator of Probability

Many traders also use delta as a rough gauge of the probability that an option will be profitable at expiration:

• A call option with a 0.30 delta suggests about a 30% chance of being profitable at expiration.
• A call option with a 0.70 delta suggests about a 70% chance of being profitable at expiration.
• At-the-money options typically have deltas around 0.50, suggesting a 50/50 chance.

This generally means traders can use delta to measure the directional risk of a given option or options strategy.

Higher deltas may be suitable for higher-risk, higher-reward strategies that are more speculative, while lower deltas may be ideally suited for lower-risk strategies with high win rates.

Gamma (Γ)

Γ Definition

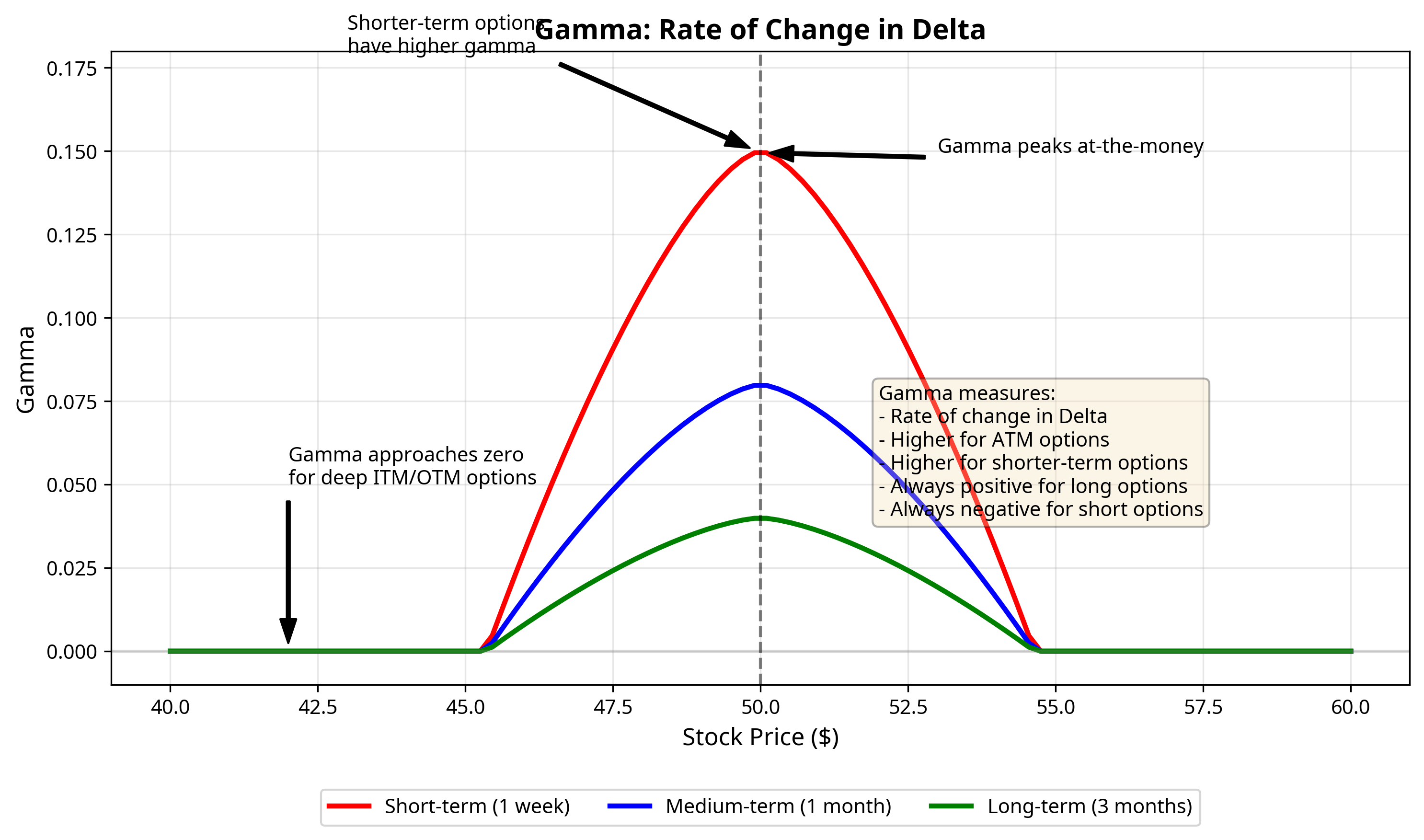
Gamma tells you how quickly delta will change when the stock price moves. Gamma values are highest for at-the-money options and lowest for those deep in-the-money (ITM) or out-of-the-money (OTM).

Characteristics

• Gamma is always positive for long options (whether calls or puts)
• Gamma is always negative for short options
• Gamma is highest for at-the-money options
• Gamma approaches zero for deep ITM or OTM options

Practical Example

Let's say you own a call option with the following details:

• Delta: 0.50
• Gamma: 0.05

If the stock rises $1, then the following occurs:

• Delta will increase by about 0.05 to 0.55
• Your option will gain about 50 cents from the initial move
• Future moves will have a slightly bigger impact because of the higher delta

Risk Implications

Suppose that two options have the same delta value, but one option has a high gamma, and one has a low gamma. The option with the higher gamma will have a higher risk since an unfavorable move in the underlying asset will have an oversized impact.

High gamma values mean that the option tends to experience volatile swings, which is bad for traders looking for predictable prospects.

Theta (Θ)

Θ Definition

Theta measures the rate of time decay in the value of an option or its premium. It quantifies how much an option's price will decrease as time passes.

Characteristics

• As time passes, the chance of an option being profitable or in-the-money decreases
• Time decay tends to accelerate as the expiration date draws closer
• Theta is always negative since time moves in the same direction
• Theta is generally good for sellers and bad for buyers

Practical Example

An option premium with no intrinsic value will decline at an increasing rate as expiration nears.

The table below shows theta values at different time intervals for an S&P 500 Dec at-the-money call option with a strike price of 930:

As you can see, theta increases as the expiration date gets closer. At T+19 (six days before expiration), theta has reached 93.3, which means the option is now losing $93.30 per day, up from $45.40 per day at T+0 when the hypothetical trader opened the position.

Trading Implications

Option buyers face a constant battle against time decay, while option sellers benefit from the passage of time. At-the-money options typically experience the most significant time decay, and this decay accelerates in the final weeks before expiration.

Vega (V)

V Definition

Vega measures the change in expectations for future volatility. It tells us how much an option's price will increase or decrease given a change in implied volatility.

Characteristics

• Higher volatility makes options more expensive since there's a greater likelihood of hitting the strike price
• Option sellers benefit from a fall in implied volatility, while option buyers benefit from a rise
• Long options have a positive vega and short options have a negative vega
• Vega can increase or decrease without price changes of the underlying asset due to changes in implied volatility
• Vega falls as the option gets closer to expiration

Practical Example

Vega is typically expressed as the dollar amount of change in the option price for a 1% change in implied volatility.

Trading Implications

When option prices are bid up because there are more buyers, implied volatility will increase. Long option traders benefit from pricing being bid up, and short option traders benefit from prices being bid down.

Traders can employ a vega-neutral position to offset the underlying asset's implied volatility. Options with longer expiration dates are generally more sensitive to volatility changes.

Rho (ρ)

ρ Definition

Rho measures an option's sensitivity to changes in the risk-free rate of interest (the interest rate paid on US Treasury bills) and is expressed as the amount of money an option will lose or gain with a 1% change in interest rates.

Characteristics

• Rho is positive for long calls (right to buy) and increases with the price of the stock
• Rho is negative for long puts (right to sell) and approaches zero as the stock price increases
• Rho is positive for short puts (obligation to buy), and negative for short calls (obligation to sell)
• Interest rate changes impact longer-term options much more than near-term options
• The higher the price of the stock and the longer time until expiration generally means a greater sensitivity to changes in interest rates

Practical Example: Positive Rho (Call Option)

⚡ Assume XYZ has a current market price of $50.00

⚡ Buying Stock Value: Buy 100 Shares XYZ at $50.00 per Share = $5,000.00 Total Cost

⚡ Buying Call Option: Buy 1 $50.00 Call at $10.00 Premium = $1,000.00 Total Cost

The total exercisable value of this option is $5,000.00 (right to buy 100 shares at $50.00). The cost to purchase the option ($1,000.00) is less upfront capital than the total exercisable value, the remaining $4,000.00 could be deposited and earn interest. This would be positively reflected in the value of the long call option as interest rates increase.

Practical Example: Negative Rho (Put Option)

⚡ XYZ has a current market price of $50.00

⚡ Shorting Stock Value: Sell 100 XYZ at $50.00 per Share = $5,000.00 Total Proceeds

⚡ Buying Put Option: Buy 1 $50.00 Put at $10.00 Premium = $1,000.00 Total Cost

The total exercisable value of this option is $5,000.00 (right to sell 100 shares at $50.00). The $5000.00 from a short sale could be deposited and earn interest. This would be negatively reflected in the value of the long put option as interest rates increase.

Trading Implications

Interest rate risk has the greatest effect on longer-dated options (LEAPS). Under normal circumstances, interest rates move gradually (~0.25% per quarter). Rho is generally less significant than other Greeks during stable interest rate environments but becomes more important in environments with significant interest rate changes.